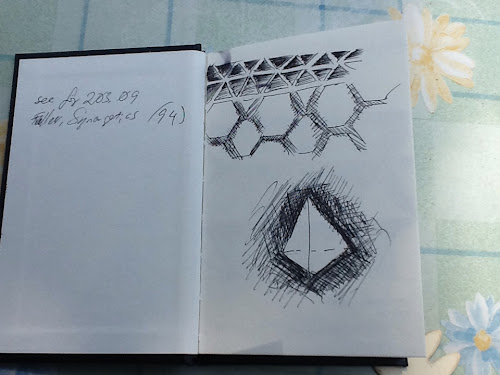Work in progress 03

These drawings get us closer to what I want to work with. The great spheres of geodesics are one point of departure, but there's also my really wanting to deal with spatial ambiguity. Plus, I've always been attracted to spirals. I'm not sure how this is going to resolve and I haven't even broached the inclusion of any naturalistic elements. More on those in the next couple of days.

Both of these started with a nautilus. I like the hidden aspect of the concentric circles in the drawing on the left, but the more pronounced spiral in the other opened me to the possibility of using it like a skeleton on which I could lay various vectors (which you can't see too well here, I don't think) and other, overlapping circles that eventually arc in opposite directions and result in those petal-like designs. This wasn't foreseen and the math is simple (they're a logical result of the iterating the movement of the arcs from starting in the center of the spiral.)

And then there's this one. Here the approach is to find a vanishing point, draw some circles around it and describe radii as overlapping arcs. When an arc is drawn through points, we have vertices of triangles that seem to lie on a torus. It's been hypothesized that one model of the universe would be a donut or a torus. This seems to be giving way to membranes and multiverses that attach to one another but don't interpenetrate (or do they?); in any event, all this stuff is providing fodder for not just this piece I want to do for my sister, but very possibly for a series of other similarly related works.

 

Posted with Blogsy

Work in progress 02

Keep the following images in mind. They may not seem to have much with geodesics or Fuller's synergetics, but remember what I said about recognizing patterns in nature and it would be worthwhile to revisit Bucky's words.

In the meantime, the two drawings are of the same subject, but different media, different context. We could assume that we are using the same initial shape, though, and that we are applying different powers of geometric progression. I'll (hopefully) make that more clear in the following section.

There's an app for that:

There's an app that uses a basic three dimensional shape and from what I can see, multiplies the shape against itself. For instance, below is a tetrahedron where n = 1.

A tetrahedron has four faces. What becomes apparent is that we have a tetrahedron as the base form, and we have an object here with twelve faces. But let's look at vertices. A tetrahedron has 9 (3 for each face). Our new figure has 36 vertices. Bear in mind that the square root of 36 is 6 and the square root of 9 is 3.

In a Fullerian context, somewhat Pythagorean in some ways, what we want to bear in mind is that Fuller was working from and working with powers of 3. But what was most telling is that he was insistent on vectors and vectors are movements/motions of force in a specific direction. To be concise, a little bit somewhat, the n values here are something like 1:4 as an exponential base.

 

Here we have n = 10.

 

 

My point in bringing this up is that we limit ourselves context by context. We tend to not recognize that what we call objects are events based on relations between other events and processes that come together and appear to us as phenomena.

What we discover as we burrow down further and further into phenomena is "less" and " less"; matter is irreducible because ultimately non-existent. Now. Work with that. More to follow.

 

Posted with Blogsy

A work in progress 01

I love my sister. That's easy. She's fun, witty, genius smarts, and a heart the size of Dallas, no, Houston, filled with wisdom and compassion. But right now, what I'm appreciating about her is that she gave me an idea, the most precious gift a human being can give another.

She was looking at paintings to put on a wall and she sent me pictures of two of them. Both were the kind corporate-favored abstraction that doesn't threaten perception or inform the viewer. And both were exorbitantly priced. Well, nuts, sez I. I can do better than both those and for loads cheaper (family discounts always apply). But mostly, looking at those pieces reminded me that nothing is abstract.

Principles aren't abstractions, for example. They tend to be deduced from patterns of behavior seen in systems at any scale or in any context where those principles obtain. I think of something Bucky Fuller wrote in part one of his masterpiece "Synergetics": "The physical Universe is a self-regenerative process. It's regenerative interrelationships and intertransformings are generated by a complex code of weightless, generalized principles. The principles are metaphysical." (Synergetics, 220.05)

A lot of what I love to do in art is join the figurative with the abstract (okay, okay...I'll defer to art history here); it could be in the handling of the material that is loose but results in a figurative whole or I've been known to render "realistically" something that doesn't exist or just play with color and line until something strikes my fancy and seems to work.

But I've reached a point in my life where I sense a kind of unifying principle behind all appearances. I realize that we live in an oftentimes binary world of dualities, most of them psychological. They way things appear aren't how things are. Indeed to even speak of things is mistaken. Again, Bucky: "There are no solids or particles -- no- things." (Ibid., 240.08)

So in throwing it out there that I'd be happy to work on a piece for my sister's wall and even sounding like an interior decorator when I asked about the color scheme, I set to work. Thinking. And meditating. Not on any one thing, just being aware and open. But I want to track the development of this piece as an inquiry into the general principle of a how a work, any work, comes to pass.

It's not by accident that I'm referring to Buckminster Fuller. He's been a huge influence on those of us of certain years and backgrounds. He was far ahead of most with his observations and maybe a little off on some, and wonderfully eccentric as an exemplar and a thinker. "Dare to be naive", he wrote. Sorry, not sure the source.

What Fuller opened up to me was grasping at the synergetic operations of the world I encounter. Not in the popular sense that the word is used in corporate boardrooms (my God, business lingo has to turned and twisted language in ways no one could fathom who thinks even a little rationally), but in its original sense from chemistry: the outcome the whole unpredicted by the action(s) of the parts. Business leader really want to use simpler terms like cooperation, but apparently prefer to sound dumber using words culled from the sciences.

Back to Bucky, though. I wondered how/if it would be possible to play with his geodesics, his tensegrities, and great circles in the context of a painting for my sister. I'm going to find out. And so will anyone else who wants to come along on the journey.

I'm keeping a small sketchbook with me, reading chunks of Fuller's works on my iPad and Chromebook and doing a study here and there in watercolor (limit is going to be six, for a reason that will be explained later.) I'm going to be lazy and order the canvas pre-stretched once I have a handful of compositions for sis to critique and choose from. In the meantime, lets begin:

The little flower is just a toss-off, but if you look closely at nature, you'll see patterns in all forms.

 

 

 

Posted with Blogsy